Given the Two Intersecting Lines Find the Solution

Method 1: Graphically

Example: Find the point of intersection for the following two lines: #{(x + y = 5), (3x + y = 1):}#

My preference for graphing lines is to write in slope intercept form, #y = mx + b#.

Written in this form, the equations are:

#y = 5 - x#
#y = 1 - 3x#

So you have slope of #-1# and y-intercept of #+5# in the first equation and slope of #-3# and y-intercept of #+1# in the second.

If we graph these two lines, we should get something like the following.

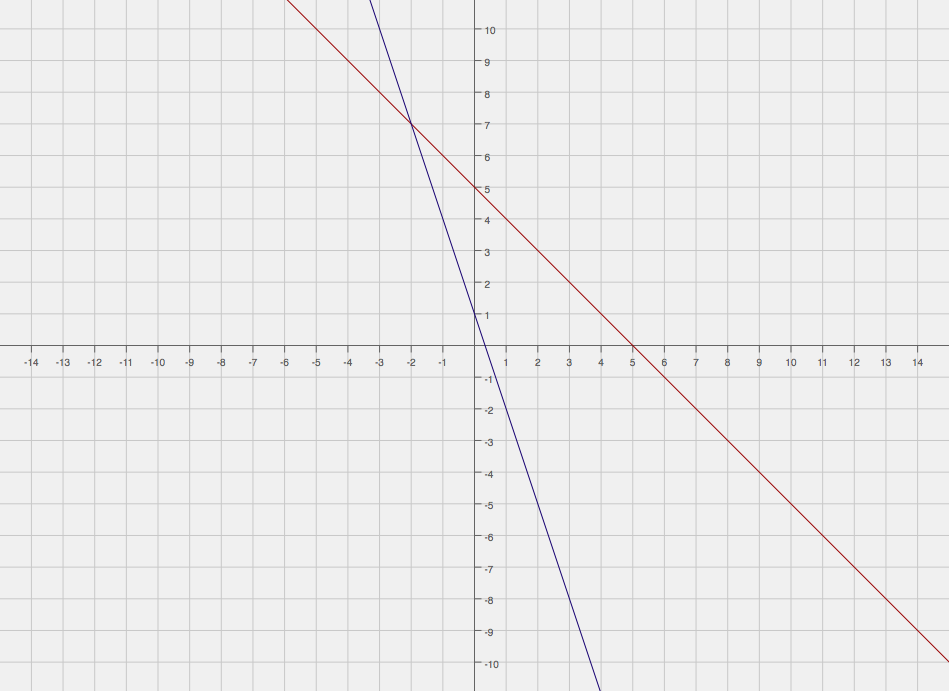
Which has intersection point #(-2, 7)#. In the case when one or both equations have coefficients of #y# that don't equal #1#, find the x and y-intercepts and graph that way.

Method 2: Algebraically

There are two methods of doing this:

•Substitution
•Elimination

Example: Solve the following system through substitution: #{(x + 3y = 5), (2x - 3y = -8):}#

The substitution method involves substituting one equation into the other, thus eliminating to one variable.

Note that from the first equation we can easily obtain #x = 5 - 3y#. Substitute this into the second equation:

#2(5 - 3y) - 3y = -8#

#10 - 6x - 3y = -8#

#-9y = -18#

#y = 2#

We can see by substitution that #x# equals #-1#:

#x + 3(2) = 5 -> x = -1#

Therefore, the solution to the given system is #(-1, 2)#.

Example: Solve the following system through elimination: #{(2x - 3y = 12), (4x + 5y = 2):}#

We often use elimination when there is no variable that is easy to isolate. Note that all of the variables in the above system have coefficients #a# where #a!= 0, 1#. This often means that if we solve for one of the variables we will end up with fractions, which can get messy.

Let's try to multiply both sides of the first equation by #-2# to see what happens.

#-2(2x - 3y) = -2(12) -> -4x + 6y =- 24#

If we add the two equations now, we get:

#0x + 11y = -22#

#y = -2#

Solve for #x# now:

#2x - 3(-2) = 12 -> 2x = 6 -> x = 3#

Therefore, the solution to the given system is #(3, -2)#.

Practice Exercises

#1#. Solve the following system of equations graphically. When the solution point is written as #(x, y)#, find the numerical value of #x + y#.

#{(2x + y = 13), (x - 3y = -11):}#

#2#. Solve the following system of equations using substitution. When the solution point is written as #(x, y)#, find the numerical value of #x+ y#.

#{(3x -3y = 21), (5x + 12y = 18):}#

#3#. Solve the following system of equations using elimination. When the solution point is written as #(x, y)#, find the numerical value of #x + y#.

#{(4x + 5y = -4), (3x + 7y = -16):}#

Solutions

#1. 9#
#2. 5#
#3. 0#

Hopefully this helps, and good luck!

Given the Two Intersecting Lines Find the Solution

Source: https://socratic.org/questions/how-can-you-find-the-intersection-of-two-lines

Share :